Global Site
Displaying present location in the site.
Graph-based Relational Learning
We can represent numerous analytics targets as graphs, where a “graph” consists of nodes representing data points and edges representing their various relationships. Diagnosing a patient, for example, not only depends on the patient’s vitals and demographic information but also on the same information about their relatives, the information about the hospitals they have visited. Predicting the future performance of a start-up not only depends on its business metrics, but also the relationships with other companies and individuals, their networks and expertise. By pushing this insight further, a team comprising NLE (NEC Laboratories Europe GmbH) and CRL (Central Research Laboratories, NEC Corporation) are in pursuit of Graph-based Relational Learning, which frames the world into graphs, and achieves groundbreaking new technologies for applications in various business do-mains. Does it not only improve the performance of node classification, but also delivers link prediction and graph classification tasks, while integrating multi-modal and incomplete data sources, and further providing explainability to complex AI models.
1. Introduction
Due to the diversity of business applications, one faces several technological challenges when applying machine learning to real-world problems with the objective of real business impact. First, it is often difficult to obtain enough labeled data. For instance, in the medical domain, it can be expensive to label data points since rare medical expertise and sometimes even wet lab experiments are required. Second, it has been recognized as increasingly important to develop interpretable and explainable machine learning methods. For instance, in the insurance business it is important to understand why a machine learning method predicts a claim to be fraudulent and the confidence it has in its prediction. Third, a multitude of available sensors leads to data points with several heterogeneous attribute types such as visual, textual, and numerical time-series features. It is challenging to combine all of these data modalities into a single machine learning model. Missing data aggravates these problems and is common in most domains including the medical and financial business domains. Finally, in order to make an AI business profitable and scalable, we need a robust data representation and processing framework that accommodates any possible use cases and is highly reuseable in other applications.
Graph-based relational learning addresses each of the above challenges by first representing the problem domain as a knowledge graph. In a second step, the graph-based learning framework we have developed is applied to the resulting graphs so as to compute solu-tions to the domain-specific problems.
The article is structured as follows. First, we introduce the meaning of graphs and their properties more formally. We show that a large number of problems can be represented as graphs. We then explain the graph-based learning framework with an emphasis on its technological innovations, setting it apart from existing competitor approaches. Finally, we present some re-cent applications of graph-based relational learning in three concrete domains for which customer trials were conducted.
2. Graph-based Relational Learning
In the following we introduce the necessary background information concerning the mathematical concept of graphs, motivate the development of graph-based machine learning algorithms, and describe the learning frameworks we have developed and applied to various use cases.
2.1 Background & Motivation
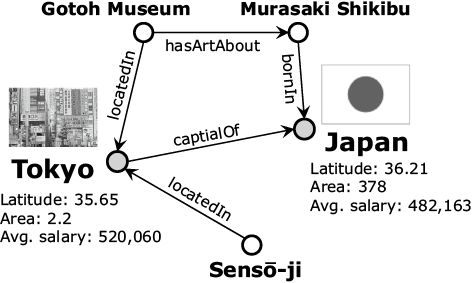
A graph consists of a set of nodes and a set of edges between these nodes. Typically, the nodes of the graph represent the data points or entities of the domain under consideration. Edges connect pairs of entities with each other and are often called relations. If a graph has multiple types of edges, it is called a multi-relational graph or knowledge graph. For instance, Fig. 1 depicts a knowledge graph with nodes corresponding to entities Tokyo, Japan, and so on, and edges representing the relations that exist between entities such as locatedIn, capitalOf, and so on.
Numerous application domains can be mapped to a graph representation. For instance, Fig. 2 depicts a graph representing a set of patients, their attributes, and the similarity between them (left) as well as a graph representing a chemical compound (right). Even if a graph representation does not exist a-priori, it can often be constructed or even learned1). For instance, it is pos-sible to construct knowledge graph representations from properly normalized relational databases.
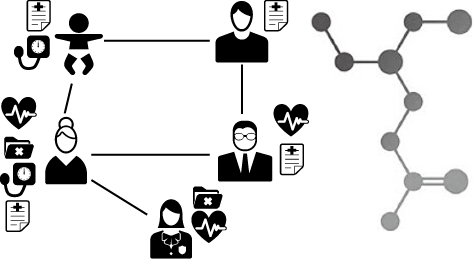
(Right) A chemical compound represented as a graph.
Once the use case is represented as a graph, we can apply graph-based relational learning to answer use case relevant prediction queries. For instance, in the example of Fig. 2, we can apply graph-based learning to predict the most probable diagnosis of a patient in the graph. This prediction is crucially influenced by the other entities the patient is connected to and does not only depend on her attributes.
2.2 Methods
In essence, we can distinguish between three prediction problems in graphs. These three prediction problems correspond to three different use case categories.
Node classification: Predicting the class label of the nodes of the graph. An example is the prediction of the disease a patient might have in Fig. 2. The input to the problem is one graph.
Link prediction: Predicting missing edges in the graph. An example is a recommender system with customers and products as nodes, and where one want to predict whether a customer node and a product node should be connected. The input to the problem is a graph.
Graph classification: Predicting the label of an entire graph. An example is predicting whether the chemical compound depicted in Fig. 2 is toxic to humans. The input to the problem is a collection of graph.
Graph-based relational learning is a framework applicable to all of these learning problems. No matter the application, it always learns vector representations of nodes and/or edges in the graph. These vector representations are often referred to as embeddings. Once the graph’s edges and nodes are represented with vectors, we can apply deep learning approaches to learn a prediction function end-to-end, using available deep learning libraries.
2.2.1 Embedding Propagation
Embedding Propagation (EP) addressed the problem of learning node vector representations for graphs with the objective to perform node classification2). In a first step, EP learns a vector representation for each attribute type by passing messages along the edges of the input graph. In the context of learning from patient data, for instance, one attribute type consists of time series data recorded for intensive care unit patients. In a second step, EP learns node representations by combining the previous learned attribute representations. These combined vector representations are then used in the downstream prediction tasks. EP is one of the first message-passing based graph neural network frameworks and exhibits superior accuracy in several semi-supervised node classification benchmark datasets2). The advantage of EP is its ability to combine various different data modalities (visual, textual, etc.) and its interpretability. Moreover, it is possible to explicitly learn vector representations of missing data. For instance, in the context of patient outcome prediction, we could show that EP is both robust to missing data and that one can determine the features most important for the predic-tion outcome3) which is crucial in the medical domain. EP has also been successfully applied to the problem of Neoantigen discovery, that is, the discovery of mutations in cancer DNA that can be used for cancer vaccine development.
2.2.2 KBLRN: The Knowledge Base Learner
The knowledge base learner (KBLRN) is a framework for link prediction, that is, for predicting missing edges in knowledge graphs4). KBLRN integrates relational, latent (learned), and numerical features, that is, features that can take on a large or infinite number of real values. The combination of various features types is achieved by integrating embedding-based learning with probabilistic models in two ways. First, KBLRN models numerical features with radial basis functions allowing these feature types to be integrated in an end-to-end differentiable learning system. Second, KBLRN uses a probabilistic product of experts (PoE)5) approach to combine the feature types. Instead of training the PoE with contrastive divergence, we approximate the partition function with a negative sampling strategy. The PoE approach has the advantage of being able to train the framework jointly and end-to-end. For every relation, there is a separate expert for each of the different feature types (Fig. 3). The scores of the three submodels (the experts for the latent, relational, and numerical features) are added and normalized.
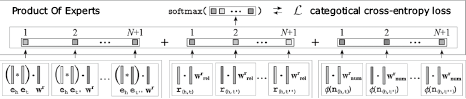
The advantages of KBLRN are its ability to combine different feature types. It is the first knowledge base learning approach that combines numerical, relational, and deep learning-based features. It was shown to have superior accuracy on a set of benchmark datasets4). Moreover, it is able to extract interpretable, rule-like features. These rules can be presented to the user and explain the predictions.
KBLRN has been applied to use cases in the public safety and financial domains. In the public safety domain it is used to answer queries about the movements of ships. In the financial domain it is used to determine whether car insurance claims are fraudulent or not. In both cases, providing explanations for the predictions is crucial. In more recent work, we have improved KBLRN to also work with visual6) and temporal information7).
2.2.3 Patchy-SAN: Graph-based Convolutional Networks
Patchy-SAN is a framework for graph representation learning, that is, for learning functions that maps graph to vector representations8). It is mainly used for the graph classification problem. Similar to convolutional neural network for images, Patchy-SAN construct locally connected neighborhoods from the input graphs. These neighborhoods are generated efficiently and serve as the receptive fields of a convolutional architecture, allowing the framework to learn effective graph representations. The proposed approach builds on concepts from convolutional neural networks (CNNs) for images9) and extends them to arbitrary graphs.
The advantage of the approach is that it is very efficient and it was shown to outperform graph kernels, the state of the art graph classification approaches at the time both in terms of processing speed and accuracy. Moreover, it is possible to visualize the extracted structural features that Patchy-SAN has learned. Fig. 4 illustrates its working.
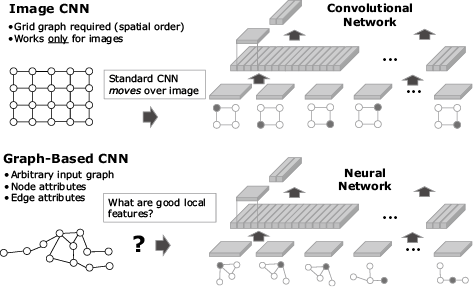
Patchy-SAN has been applied to problems from the biomedical domain such as small chemical compound classification where it outperformed state of the art approaches. It can also be used to compute similarities between graphs, something that can be used to match graphs, an important problem in biometrics.
3. Conclusion
A team comprised of members from CRL and NLE has developed a general framework for graph-based machine learning. By framing the real-word tasks into graph prediction problems, the technology has shown to address a wide range of business domains.
4. Acknowledgement
Here we would like to extend our acknowledgement to the contribution from NLE and CRL members, namely Kazeto Yamamoto, Yuzuru Okajima, Daichi Kimura and others, whose contribution was behind the successful execution of the project.
References
- 1)Luca Franceschi, Mathias Niepert, Massimiliano Pontil, Xiao He: Learning Discrete Structures for Graph Neural Networks, the 36th International Conference on Machine Learning (ICML)
- 2)Alberto Garcia-Duran and Mathias Niepert: Learning Graph Representations with Embedding Propagation, the 31st Annual Conference on Neural Information Processing Systems (NIPS), 2017
- 3)Brandon Malone, Alberto Garcia-Duran, and Mathias Niepert: Learning Representations of Missing Data for Predicting Patient Outcomes, 2018
- 4)Alberto Garcia-Duran and Mathias Niepert: KBLRN: End-to-End Learning of Knowledge Base Representations with Latent, Relational, and Numerical Features, the 34th Conference on Uncertainty in Artificial Intelligence (UAI)
- 5)G. E. Hinton: Training products of experts by minimizing contrastive divergence, Neural computation, vol.14 Issue 8, pp.1771–1800, 2002
- 6)Daniel Oñoro-Rubio, Mathias Niepert, Alberto García-Durán, Roberto González, Roberto J. López-Sastre: Answering Visual-Relational Queries in Web-Extracted Knowledge Graphs. In Proceedings of the 1st Conference on Automated Knowledge Base Construction (AKBC)
- 7)Alberto Garcia-Duran, Sebastijan Dumancic, and Mathias Niepert: Learning Sequence Encoders for Temporal Knowledge Base Completion. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP)
- 8)Mathias Niepert, Mohamed Ahmed, and Konstantin Kutzkov: Learning Convolutional Neural Networks for Graphs, the 33rd International Conference on Machine Learning (ICML), 2016
- 9)Fukushima Kunihiko: Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position, Biological Cybernetics, Vol.36 Issue 4, pp.193–202, 1980
Authors’ Profiles
Chief Researcher
NEC Laboratories Europe GmbH
Research Scientist
NEC Laboratories Europe GmbH
Ecole Polytechnique Fédérale de Lau-sanne
Senior Researcher
NEC Laboratories Europe GmbH
Senior Researcher
NEC Laboratories Europe GmbH
Deputy General Manager
NEC Laboratories Europe GmbH
Principal Researcher
Security Research Laboratories
Senior Manager
Security Research Laboratories
Principal Researcher
Security Research Laboratories
Research Fellow
Data Science Research Laboratories
General Manager
NEC Laboratories Europe GmbH